In Preliminary Finals since 2000 teams finishing in ladder position 1 are now 3-0 over teams finishing 3rd, and teams finishing in ladder position 2 are 5-0 over teams finishing 4th.
Overall in Preliminary Finals, teams finishing in 1st now have a 70% record, teams finishing 2nd an 80% record, teams finishing 3rd a 38% record, and teams finishing 4th a measly 20% record. This generally poor showing by teams from 3rd and 4th has meant that we've had at least 1 of the top 2 teams in every Grand Final since 2000.
Reviewing the middle table in the diagram above we see that there have been 4 Grand Finals since 2000 involving the teams from 1st and 2nd on the ladder and these contests have been split 2 apiece. No other pairing has occurred with a greater frequency.
Two of these top-of-the-table clashes have come in the last 2 seasons, with 1st-placed Geelong defeating 2nd-placed Port Adelaide in 2007, and 2nd-placed Hawthorn toppling 1st-placed Geelong last season. Prior to that we need to go back firstly to 2004, when 1st-placed Port Adelaide defeated 2nd-placed Brisbane Lions, and then to 2001 when 1st-placed Essendon surrendered to 2nd-placed Brisbane Lions.
Ignoring the replays of 1948 and 1977 there have been 110 Grand Finals in the 113-year history of the VFL/AFL history, with Grand Finals not being used in the 1897 or 1924 seasons. The pairings and win-loss records for each are shown in the table below.
As you can see, this is the first season that St Kilda have met Geelong in the Grand Final. Neither team has been what you'd call a regular fixture at the G come Grand Final Day, though the Cats can lay claim to having been there more often (15 times to the Saints' 5) and to having a better win-loss percentage (47% to the Saints' 20%).
After next weekend the Cats will move ahead of Hawthorn into outright 7th in terms of number of GF appearances. Even if they win, however, they'll still trail the Hawks by 2 in terms of number of Flags.
So far we've learned that handicap-adjusted margins appear to be normally distributed with a mean of zero and a standard deviation of 37.7 points. That means that the unadjusted margin - from the favourite's viewpoint - will be normally distributed with a mean equal to minus the handicap and a standard deviation of 37.7 points. So, if we want to simulate the result of a single game we can generate a random Normal deviate (surely a statistical contradiction in terms) with this mean and standard deviation.
Alternatively, we can, if we want, work from the head-to-head prices if we're willing to assume that the overround attached to each team's price is the same. If we assume that, then the home team's probability of victory is the head-to-head price of the underdog divided by the sum of the favourite's head-to-head price and the underdog's head-to-head price.
So, for example, if the market was Carlton $3.00 / Geelong $1.36, then Carlton's probability of victory is 1.36 / (3.00 + 1.36) or about 31%. More generally let's call the probability we're considering P%.
Working backwards then we can ask: what value of x for a Normal distribution with mean 0 and standard deviation 37.7 puts P% of the distribution on the left? This value will be the appropriate handicap for this game.
Again an example might help, so let's return to the Carlton v Geelong game from earlier and ask what value of x for a Normal distribution with mean 0 and standard deviation 37.7 puts 31% of the distribution on the left? The answer is -18.5. This is the negative of the handicap that Carlton should receive, so Carlton should receive 18.5 points start. Put another way, the head-to-head prices imply that Geelong is expected to win by about 18.5 points.
With this result alone we can draw some fairly startling conclusions.
In a game with prices as per the Carlton v Geelong example above, we know that 69% of the time this match should result in a Geelong victory. But, given our empirically-based assumption about the inherent variability of a football contest, we also know that Carlton, as well as winning 31% of the time, will win by 6 goals or more about 1 time in 14, and will win by 10 goals or more a litle less than 1 time in 50. All of which is ordained to be exactly what we should expect when the underlying stochastic framework is that Geelong's victory margin should follow a Normal distribution with a mean of 18.8 points and a standard deviation of 37.7 points.
So, given only the head-to-head prices for each team, we could readily simulate the outcome of the same game as many times as we like and marvel at the frequency with which apparently extreme results occur. All this is largely because 37.7 points is a sizeable standard deviation.
Well if simulating one game is fun, imagine the joy there is to be had in simulating a whole season. And, following this logic, if simulating a season brings such bounteous enjoyment, simulating say 10,000 seasons must surely produce something close to ecstasy.
I'll let you be the judge of that.
Anyway, using the Wednesday noon (or nearest available) head-to-head TAB Sportsbet prices for each of Rounds 1 to 20, I've calculated the relevant team probabilities for each game using the method described above and then, in turn, used these probabilities to simulate the outcome of each game after first converting these probabilities into expected margins of victory.
(I could, of course, have just used the line betting handicaps but these are posted for some games on days other than Wednesday and I thought it'd be neater to use data that was all from the one day of the week. I'd also need to make an adjustment for those games where the start was 6.5 points as these are handled differently by TAB Sportsbet. In practice it probably wouldn't have made much difference.)
Next, armed with a simulation of the outcome of every game for the season, I've formed the competition ladder that these simulated results would have produced. Since my simulations are of the margins of victory and not of the actual game scores, I've needed to use points differential - that is, total points scored in all games less total points conceded - to separate teams with the same number of wins. As I've shown previously, this is almost always a distinction without a difference.
Lastly, I've repeated all this 10,000 times to generate a distribution of the ladder positions that might have eventuated for each team across an imaginary 10,000 seasons, each played under the same set of game probabilities, a summary of which I've depicted below. As you're reviewing these results keep in mind that every ladder has been produced using the same implicit probabilities derived from actual TAB Sportsbet prices for each game and so, in a sense, every ladder is completely consistent with what TAB Sportsbet 'expected'.
The variability you're seeing in teams' final ladder positions is not due to my assuming, say, that Melbourne were a strong team in one season's simulation, an average team in another simulation, and a very weak team in another. Instead, it's because even weak teams occasionally get repeatedly lucky and finish much higher up the ladder than they might reasonably expect to. You know, the glorious uncertainty of sport and all that.
Consider the row for Geelong. It tells us that, based on the average ladder position across the 10,000 simulations, Geelong ranks 1st, based on its average ladder position of 1.5. The barchart in the 3rd column shows the aggregated results for all 10,000 simulations, the leftmost bar showing how often Geelong finished 1st, the next bar how often they finished 2nd, and so on.
The column headed 1st tells us in what proportion of the simulations the relevant team finished 1st, which, for Geelong, was 68%. In the next three columns we find how often the team finished in the Top 4, the Top 8, or Last. Finally we have the team's current ladder position and then, in the column headed Diff, a comparison of the each teams' current ladder position with its ranking based on the average ladder position from the 10,000 simulations. This column provides a crude measure of how well or how poorly teams have fared relative to TAB Sportsbet's expectations, as reflected in their head-to-head prices.
Here are a few things that I find interesting about these results:
(In another blog I've used the same simulation methodology to simulate the last two rounds of the season and project where each team is likely to finish.)
The curse of the unbalanced draw remains in the AFL this year and teams will once again finish in ladder positions that they don't deserve. As long-time MAFL readers will know, this is a topic I've returned to on a number of occasions but, in the past, I've not attempted to quantify its effects.
This week, however, a MAFL Investor sent me a copy of a paper that's been prepared by Liam Lenten of the School of Economics and Finance at La Trobe University for a Research Seminar Series to be held later this month and in which he provides a simple methodology for projecting how each team would have fared had they played the full 30-game schedule, facing every other team twice.
For once I'll spare you the details of the calculation and just provide an overview. Put simply, Lenten's method adjusts each team's actual win ratio (the proportion of games that it won across the entire season counting draws as one-half a win) based on the average win ratios of all the teams it met only once. If the teams it met only once were generally weaker teams - that is, teams with low win ratios - then its win ratio will be adjusted upwards to reflect the fact that, had these weaker teams been played a second time, the team whose ratio we're considering might reasonably have expected to win a proportion of them greater than their actual win ratio.
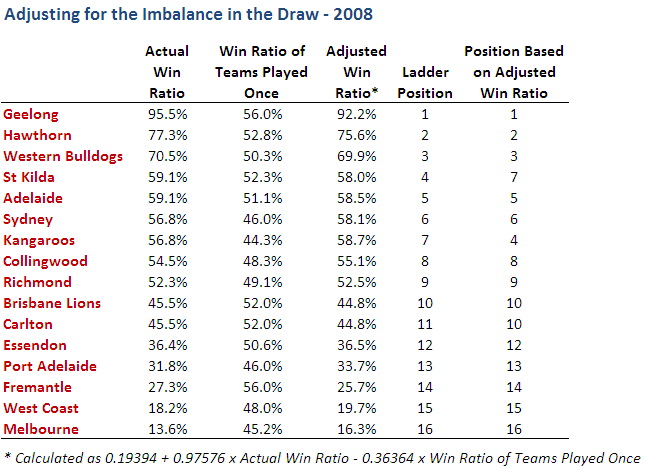
As ever, an example might help. So, here's the detail for last year.
Consider the row for Geelong. In the actual home and away season they won 21 from 22 games, which gives them a win ratio of 95.5%. The teams they played only once - Adelaide, Brisbane Lions, Carlton, Collingwood, Essendon, Hawthorn, St Kilda and the Western Bulldogs - had an average win ratio of 56.0%. Surprisingly, this is the highest average win ratio amongst teams played only once for any of the teams, which means that, in some sense, Geelong had the easiest draw of all the teams. (Although I do again point out that it benefited heavily from not facing itself at all during the season, a circumstance not enjoyed by any other team.)
The relatively high average win ratio of the teams that Geelong met only once serves to depress their adjusted win ratio, moving it to 92.2%, still comfortably the best in the league.
Once the calculations have been completed for all teams we can use the adjusted win ratios to rank them. Comparing this ranking with that of the end of season ladder we find that the ladder's 4th-placed St Kilda swap with the 7th-placed Roos and that the Lions and Carlton are now tied rather than being split by percentages as they were on the actual end of season ladder. So, the only significant difference is that the Saints lose the double chance and the Roos gain it.
If we look instead at the 2007 season, we find that the Lenten method produces much greater change.
In this case, eight teams' positions change - nine if we count Fremantle's tie with the Lions under the Lenten method. Within the top eight, Port Adelaide and West Coast swap 2nd and 3rd, and Collingwood and Adelaide swap 6th and 8th. In the bottom half of the ladder, Essendon and the Bulldogs swap 12th and 13th, and, perhaps most important of all, the Tigers lose the Spoon and the priority draft pick to the Blues.
In Lenten's paper he looks at the previous 12 seasons and finds that, on average, five to six teams change positions each season. Furthermore, he finds that the temporal biases in the draw have led to particular teams being regularly favoured and others being regularly handicapped. The teams that have, on average, suffered at the hands of the draw have been (in order of most affected to least) Adelaide, West Coast, Richmond, Fremantle, Western Bulldogs, Port Adelaide, Brisbane Lions, Kangaroos, Carlton. The size of these injustices range from an average 1.11% adjustment required to turn Adelaide's actual win ratio into an adjusted win ratio, to just 0.03% for Carlton.
On the other hand, teams that have benefited, on average, from the draw have been (in order of most benefited to least) Hawthorn, St Kilda, Essendon, Geelong, Collingwood, Sydney and Melbourne. Here the average benefits range from 0.94% for Hawthorn to 0.18% for Melbourne.
I don't think that the Lenten work is the last word on the topic of "unbalance", but it does provide a simple and reasonably equitable way of quantitatively dealing with its effects. It does not, however, account for any inter-seasonal variability in team strengths nor, more importantly, for the existence any home ground advantage.
Still, if it adds one more finger to the scales on the side of promoting two full home and away rounds, it can't be a bad thing can it?
It's time to consider the grand sweep of football history once again.
This time I'm looking at the teams' finishing positions, in particular the number and proportion of times that they've each finished as Premiers, Wooden Spooners, Grand Finalists and Finalists, or that they've finished in the Top Quarter or Top Half of the draw.
Here's a table providing the All-Time data.
Note that the percentage columns are all as a percentage of opportunities. So, for a season to be included in the denominator for a team's percentage, that team needs to have played in that season and, in the case of the Grand Finalists and Finalists statistics, there needs to have been a Grand Final (which there wasn't in 1897 or 1924) or there needs to have been Finals (which, effectively, there weren't in 1898, 1899 or 1900).
Looking firstly at Premierships, in pure number terms Essendon and Carlton tie for the lead on 16, but Essendon missed the 1916 and 1917 seasons and so have the outright lead in terms of percentage. A Premiership for West Coast in any of the next 5 seasons (and none for the Dons) would see them overtake Essendon on this measure.
Moving then to Spoons, St Kilda's title of the Team Most Spooned looks safe for at least another half century as they sit 13 clear of the field, and University will surely never relinquish the less euphonius but at least equally as impressive title of the Team With the Greatest Percentage of Spooned Seasons. Adelaide, Port Adelaide and West Coast are the only teams yet to register a Spoon (once the Roos' record is merged with North Melbourne's).
Turning next to Grand Finals we find that Collingwood have participated in a remarkable 39 of them, which equates to a better than one season in three record and is almost 10 percentage points better than any other team. West Coast, in just 22 seasons, have played in as many Grand Finals as have St Kilda, though St Kilda have had an additional 81 opportunities.
The Pies also lead in terms of the number of seasons in which they've participated in the Finals, though West Coast heads them in terms of percentages for this same statistic, having missed the Finals less than one season in four across the span of their existence.
Finally, looking at finishing in the Top Half or Top Quarter of the draw we find the Pies leading on both of these measures in terms of number of seasons but finishing runner-up to the Eagles in terms of percentages.
The picture is quite different if we look just at the 1980 to 2008 period, the numbers for which appear below.
Hawthorn now dominates the Premiership, Grand Finalist and finishing in the Top Quarter statistics. St Kilda still own the Spoon market and the Dons lead in terms of being a Finalist most often and finishing in the Top Half of the draw most often.
West Coast is the team with the highest percentage of Finals appearances and highest percentage of times finishing in the Top Half of the draw.
Last year, 20 games in the home and away season were decided by less than a goal and two teams, Richmond and Sydney were each involved in 5 of them.
Relatively speaking, the Tigers and the Swans fared quite well in these close finishes, each winning three, drawing one and losing just one of the five contests.
Fremantle, on the other hand, had a particularly bad run in close games last years, losing all four of those it played in, which contributed to an altogether forgettable year for the Dockers.
The table below shows each team's record in close games across the previous five seasons.
Surprisingly, perhaps, the Saints head the table with a 71% success rate in close finishes across the period 2004-2008. They've done no worse than 50% in close finishes in any of the previous five seasons, during which they've made three finals appearances.
Next best is West Coast on 69%, a figure that would have been higher but for an 0 and 1 performance last year, which was also the only season in the previous five during which they missed the finals.
Richmond have the next best record, despite missing the finals in all five seasons. They're also the team that has participated in the greatest number of close finishes, racking up 16 in all, one ahead of Sydney, and two ahead of Port.
The foot of the table is occupied by Adelaide, whose 3 and 9 record includes no season with a better than 50% performance. Nonetheless they've made the finals in four of the five years.
Above Adelaide are the Hawks with a 3 and 6 record, though they are 3 and 1 for seasons 2006-2008, which also happen to be the three seasons in which they've made the finals.
So, from what we've seen already, there seems to be some relationship between winning the close games and participating in September's festivities. The last two rows of the table shed some light on this issue and show us that Finalists have a 58% record in close finishes whereas Non-Finalists have only a 41% record.
At first, that 58% figure seems a little low. After all, we know that the teams we're considering are Finalists, so they should as a group win well over 50% of their matches. Indeed, over the five year period they won about 65% of their matches. It seems then that Finalists fare relatively badly in close games compared to their overall record.
However, some of those close finishes must be between teams that both finished in the finals, and the percentage for these games is by necessity 50% (since there's a winner and a loser in each game, or two teams with draws). In fact, of the 69 close finishes in which Finalists appeared, 29 of them were Finalist v Finalist matchups.
When we look instead at those close finishes that pitted a Finalist against a Non-Finalist we find that there were 40 such clashes and that the Finalist prevailed in about 70% of them.
So that all seems as it should be.
In a comment on the previous posting, Mitch asked if we could take a look at each team's performance by era, his interest sparked by the strong all-time performance of the Blues and his recollection of their less than stellar recent seasons.
Here's the data:
So, as you can see, Carlton's performance in the most recent epoch is significantly below its all-time performance. In fact, the 1993-2008 epoch is the only one in which the Blues failed to return a better than 50% performance.
Collingwood, the only team with a better lifetime record than Carlton, have also had a well below par last epoch during which they too have registered their first sub-50% performance, continuing a downward trend which started back in Epoch 2.
Six current teams have performed significantly better in the 1993-2008 epoch than their all-time performance: Geelong (who registered their best ever epoch), Sydney (who cracked 50% for the first time in four epochs), Brisbane (who could hardly but improve), the Western Bulldogs (who are still yet to break 50% for an epoch, their 1945-1960 figure being actually 49.5%), North Melbourne (who also registered their best ever epoch), and St Kilda (who still didn't manage 50% for the epoch, a feat they've achieved only once).
Just before we wind up I should note that the 0% for University in Epoch 2 is not an error. It's the consequence of two 0 and 18 performances by Uni in 1913 and 1914 which, given that these followed directly after successive 1 and 17 performances in 1911 and 1912, unsurprisingly heralded the club's demise. Given that Uni's sole triumph of 1912 came in the third round, by my calculations that means University lost its final 51 matches.
At this time of year, before we fixate on the week-to-week triumphs and travesties of yet another AFL season, it's interesting to look at the varying fortunes of all the teams that have ever competed in the VFL/AFL.
The table below provides the Win, Draw and Loss records of every team.
As you can see, Collingwood has the best record of all the teams having won almost 61% of all the games in which it has played, a full 1 percentage point better than Carlton, in second. Collingwood have also played more games than any other team and will be the first team to have played in 2,300 games when Round 5 rolls around this year.
Amongst the relative newcomers to the competition, West Coast and Port Adelaide - and to a lesser extent, Adelaide - have all performed well having won considerably more than half of their matches.
Sticking with newcomers but dipping down to the other end of the table we find Fremantle with a particularly poor record. They've won just under 40% of their games and, remarkably, have yet to register a draw. (Amongst current teams, Essendon have recorded the highest proportion of drawn games at 1.43%, narrowly ahead of Port Adelaide with 1.42%. After Fremantle, the team with the next lowest proportion of drawn games is Adelaide at 0.24%. In all, 1.05% of games have finished with scores tied.)
Lower still we find the Saints, a further 1.3 percentage points behind Fremantle. It took St Kilda 48 games before it registered its first win in the competition, which should surely have been some sort of a hint to fans of the pain that was to follow across two world wars and a depression (maybe two). Amongst those 112 seasons of pain there's been just the sole anaesthetising flag, in 1966.
Here then are a couple of milestones that we might witness this year that will almost certainly go unnoticed elsewhere:
Granted, few of those are truly banner events, but if AFL commentators were as well supported by statisticians as, say, Major League Baseball, you can bet they'd get a mention, much as equally arcane statistics are sprinkled liberally in the 3 hours of dead time there is between pitches.
With the pre-season now underway it's only right that I revisit the topic of the extent to which pre-season performance predicts regular season success.
Here's the table with the relevant data:
The macro view tells us that, of the 21 pre-season winners, only 14 of them have gone on to participate in the regular season finals in the same year and, of the 21 pre-season runners-up, only 12 of them have made that same category. When you consider that roughly one-half of the teams have made the regular season finals in each year - slightly less from 1988 to 1993, and slightly more in 1994 - those stats look fairly unimpressive.
But a closer, team-by-team view shows that Carlton alone can be blamed for 3 of the 7 occasions on which the pre-season winner has missed the regular season finals, and Adelaide and Richmond can be blamed for 4 of the 9 occasions on which the pre-season runner-up has missed the regular season finals.
So, unless you're a Crows, Blues or Tigers supporter, you should be at least a smidge joyous if your team makes the pre-season final; if history's any guide, the chances are good that your team will get a ticket to the ball in September.
It's one thing to get a ticket but another thing entirely to steal the show. Pre-season finalists can, collectively, lay claim to five flags but, as a closer inspection of the previous table will reveal, four of these flags have come from just two teams, Essendon and Hawthorn. What's more, no flag has come to a pre-season finalist since the Lions managed it in 2001.
On balance then, I reckon I'd rather the team that I supported remembered that there's a "pre" in pre-season.
Well I guess it's about time we had a look at the AFL draw for 2009.
I've summarised it in the following schematic:
The numbers show how many times a particular matchup occurs at home, away or at a neutral venue in terms of the team shown in the leftmost column. So, for example, looking at the first row, Adelaide play the Lions only once during 2009 and it's an away game for Adelaide.
For the purpose of assessing the relative difficulty of each team's schedule, I'll use the final MARS Ratings for 2008, which were as follows:
Given those, the table below shows the average MARS Rating of the opponents that each team faces at home, away and at neutral venues.
So, based solely on average opponent rating, regardless of venue, the Crows have the worst of the 2009 draw. The teams they play only once include five of the bottom six MARS-ranked teams in Brisbane (11th), Richmond (12th), Essendon (14th), West Coast (15th), Melbourne (16th). One mitigating factor for the Crows is that they tend to play stronger teams at home: they have the 2nd toughest home schedule and only the 6th toughest away and neutral-venue schedules.
Melbourne fare next worst in the draw, meeting just once four of the bottom five teams, excluding themselves. They too, however, tend to face stronger teams at home and relatively weaker teams away, though their neutral-venue schedule is also quite tough (St Kilda and Sydney).
Richmond, in contrast, get the best of the draw, avoiding a second contest with six of the top eight teams and playing each of the bottom four teams twice.
St Kilda's draw is the next best and sees them play once only four of the teams in the top eight and play each of the bottom three teams twice.
Looking a little more closely and differentiating home games from away games, we find that the Bulldogs have the toughest home schedule but also the easiest away schedule. Port Adelaide have the easiest home schedule and Sydney have the toughest away schedule.
Generally speaking, last year's finalists have fared well in the draw, with five of them having schedules ranked 10th or lower. Adelaide, Sydney and, to a lesser extent, the Bulldogs are the exceptions. It should be noted that higher-ranked teams always have a relative advantage over other teams in that their schedules exclude games against themselves.
Over the break I came across what must surely be amongst the simplest, most practical team rating systems.
It's based on the general premise that a team's rating should be proportional to the sum of the ratings of the teams that it has defeated. In the variant that I've used, each team's rating is proportional to the rating of those teams it has defeated on each occasion that it has faced them in a given season plus one-half of the rating of those teams with which it has drawn if they played only once, or with which it has won once and lost once if they have played twice during the season.
(Note that I've used only regular home-and-away season games for these ratings and that I've made no allowance for home team advantage.)
This method produces relative, not absolute, ratings so we can arbitrarily set any one team's rating - say the strongest team's - to be 1, and then define every other team's rating relative to this. All ratings are non-negative.
Using the system requires some knowledge of matrix algebra, but that's about it. (For the curious, the ratings involve solving the equation Ax = kx where A is a symmetric matrix with 0s on the diagonal and where Aij is the proportion of games between teams i and j that were won by i and Aji = 1 - Aij; x is the ratings vector; and k is a constant. The solution for x that we want is the first-rank eigenvector of A. We normalise x by dividing each element by the maximum element in x.)
Applying this technique to the home-and-away games of the previous 10 seasons, we obtain the following ratings:
Now bear in mind that it makes little sense to directly compare ratings across seasons, so a rating of, say, 0.8 this year means only that the team was in some sense 80% as good as the best team this year; it doesn't mean that the team was any better or worse than a team rating 0.6 last year unless you're willing to make some quantitative assumption about the relative merits of this year's and last year's best teams.
What we can say with some justification however is that Geelong was stronger relative to Port in 2007 than was Geelong relative to the Hawks in 2008, The respective GFs would seem to support this assertion.
So, looking across the 10 seasons, we find that:
Perhaps most important of all we can say that the Brisbane Lions are the Team of the Decade.
Here is the ratings table above in ranking form:
What's interesting about these rankings from a Brisbane Lions point of view is that only twice has its rating been 10th or worse. Of particular note is that, in seasons 2005 and 2008, Brisbane rates in the top 8 but did not make the finals. In 2008 the Lions won all their encounters against 3 of the finalists and shared the honours with 2 more, so there seems to be some justification for their lofty 2008 rating at least.
Put another way, based on the ratings, Brisbane should have participated in all but 2 of the past 10 final series. No other team can make that claim.
Second-best Team of the Decade is Port Adelaide, who registered 3 consecutive Highest Rated Team across seasons 2002, 2003 and 2004. Third-best is Geelong, largely due to their more recent performance, which has seen them amongst the top 5 teams in all but 1 of the previous 5 seasons.
The Worst Team of the Decade goes to Carlton, who've finished ranked 10th or below in each of the previous 7 seasons. Next worst is Richmond who have a similar record blemished only by a 9th-placed finish in 2006.
MAFL is a website for ...
(For those not wanting to use PayPal, my email address below is now also a PayID)
Click on the envelope
Copyright © 2006-2025, Tony Corke. All rights reserved.
