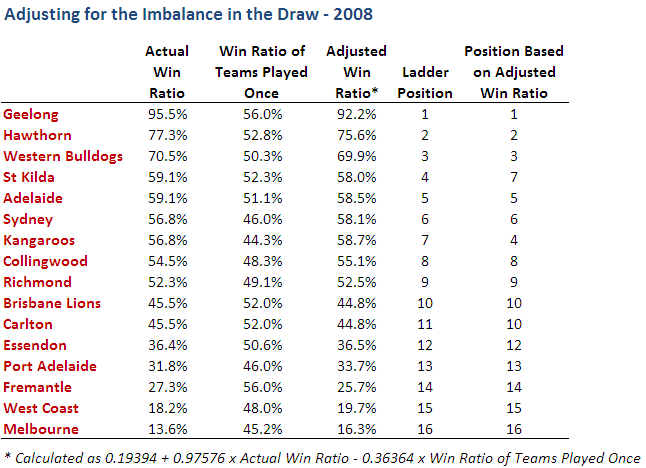
In this case, eight teams' positions change - nine if we count Fremantle's tie with the Lions under the Lenten method. Within the top eight, Port Adelaide and West Coast swap 2nd and 3rd, and Collingwood and Adelaide swap 6th and 8th. In the bottom half of the ladder, Essendon and the Bulldogs swap 12th and 13th, and, perhaps most important of all, the Tigers lose the Spoon and the priority draft pick to the Blues.
In Lenten's paper he looks at the previous 12 seasons and finds that, on average, five to six teams change positions each season. Furthermore, he finds that the temporal biases in the draw have led to particular teams being regularly favoured and others being regularly handicapped. The teams that have, on average, suffered at the hands of the draw have been (in order of most affected to least) Adelaide, West Coast, Richmond, Fremantle, Western Bulldogs, Port Adelaide, Brisbane Lions, Kangaroos, Carlton. The size of these injustices range from an average 1.11% adjustment required to turn Adelaide's actual win ratio into an adjusted win ratio, to just 0.03% for Carlton.
On the other hand, teams that have benefited, on average, from the draw have been (in order of most benefited to least) Hawthorn, St Kilda, Essendon, Geelong, Collingwood, Sydney and Melbourne. Here the average benefits range from 0.94% for Hawthorn to 0.18% for Melbourne.
I don't think that the Lenten work is the last word on the topic of "unbalance", but it does provide a simple and reasonably equitable way of quantitatively dealing with its effects. It does not, however, account for any inter-seasonal variability in team strengths nor, more importantly, for the existence any home ground advantage.
Still, if it adds one more finger to the scales on the side of promoting two full home and away rounds, it can't be a bad thing can it?