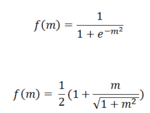Building Your Own Team Rating System
/Just before the 2nd Round of 2008 I created MAFL's Team Ratings System, MARS, never suspecting that I'd still be writing about it 5 years later. At the time, I described MARS in the newsletter for that week in a document still available from the Newsletters 2005-2008 section of this website (it's linked under the "MAFL The Early Years" menu item in the navigation bar on the right of screen). Since then, MARS, as much to my surprise as I think to anyone's, has been a key input to the Line Funds that have operated in each of the ensuing years.
Lately, perhaps due to the relative success of those Funds, I've seen an increase in traffic to the MAFL website that appears to have been motivated by an interest in the topic of team ratings. Whilst the 2008 Newsletter revealed a little about the process I went through in creating MARS, it didn't discuss the alternatives that were available to me nor provide substantive guidance for anyone thinking about building a Rating System of their own.
Buoyed by this recent interest, I've created today's blog posting to help anyone contemplating the creation of their own Rating System, and for anyone who is generally interested in understanding in more depth some of the considerations that go into creating such a System.
Elo Is Not a Dirty Word
(Younger and international visitors please see http://www.youtube.com/watch?v=UduuxKdPt9Q for the source of the appalling pun in that title.)
MARS, you might recall, is an Elo-type Rating System. The Elo System was developed as an improved method "for calculating the relative skill levels of players in competitor-versus-competitor games". It was specifically designed to rate chess players but can easily be applied to other person-versus-person and team-versus-team situations.
The philosophy at the heart of any Elo System holds that:
A team's (or player's) Rating is updated at the end of each contest or set of contests.
Rating changes are "zero-sum" in that the Ratings gain of one participant in a contest is exactly matched by the Ratings loss of its opponent.
The merit of any performance is measured relative to the quality of the opponent faced. Defeating - or in some way doing better than - a relatively stronger opponent is rewarded more lavishly than a similar performance achieved when facing a more evenly-matched or a weaker opponent.
An Elo-style approach to team ratings is by no means the only one possible, and many other types exist such as the Massey and Colley Systems, and the Offence-Defence Model (ODM), all of which are described elsewhere on MAFL and tracked during the course of each AFL season. In this blog, I'll be talking solely about Elo-style Rating systems.
(If you're looking for a well-written book on the topic of Team Rating Systems that are similar to Massey, Colley and the ODM, I can recommend Who's #1 by Langville and Meyer.)
Rating Updates: The Basic Equation
The first equation in any Elo-type System is the one used for updating Team Ratings on the basis of some outcome.
In words, a team's updated Rating is equal to the Rating it carried into the contest plus some multiple, k, of the difference between the Actual Outcome of the game - suitably defined - and the Expected Outcome, with both Outcomes being measured from the viewpoint of the team whose Rating is being updated.
The parameter k, which takes on only positive values, can be selected by the System Creator and is a "stretching" parameter that determines the extent to which Team Ratings respond to over- and under-achievement relative to expectation. Larger values of k make the resulting System more responsive to unexpected achievement, so Team Ratings will tend to move more on the basis of a single result, while smaller values of k result in Systems with the opposite characteristic - that is, with Ratings that are more 'sticky' and less responsive to the outcome of a single contest. We can think of the value of k as determining the extent to which the resulting Rating System tracks form (large k) or tracks class (small k).
Step 1: Choosing an Outcome Measure
The basic equation described earlier is contingent on the choice of some game outcome. This outcome can be any quantifiable measure of a game, the choice you make determining what it is that, essentially, the resultant Rating System actually rates.
One obvious choice for this outcome measure is the result of the contest, win, draw or loss. For the Actual Outcome term we might then quantify that outcome as 1 for a win, 0.5 for a draw, and 0 for a loss. We could then conceptualise the Expected Outcome as a measure of a team's pre-game probability of victory. This choice of outcome measure is the one used in the basic Elo System.
Mathematically, in generalising the Elo System as I'm doing in this blog, there's no strict need to constrain the range of the Actual Outcome variable or of the feasible values of (Actual Outcome - Expected Outcome) in the basic equation above. But, for my purposes, I'm going to assume that whatever outcome measure you choose will be constrained or transformed to lie in the interval 0 to 1 with better performances resulting in Actual Outcomes nearer 1 and worse performances resulting in Actual Outcomes nearer 0.
I'll also assume that the Expected Outcome measure will be constrained to this same interval, thus also constraining the size of the (Actual Outcome - Expected Outcome) term and preventing Team Ratings from "exploding" as Ratings are updated over a series of contests. (We could also, of course, effectively constrain the impact of the difference between Actual and Expected outcomes, achieving much the same result as we obtain in bounding the ranges for the Actual and Expected Outcome terms, by choosing a suitable value of k.)
Now, instead of choosing the game result as our outcome measure we might rather choose a transformed version of the team's margin of victory. This is the outcome measure I use in MAFL's MARS Rating System, where I transform a capped version of the victory margin, truncating any victory margins in excess of 78 points. (Capping is employed to limit the size of Rating changes that result from blowout victories, the thinking being that a victory by, say, 100 points provides no more information about the relative merits of the two teams that produced that outcome than does a victory by 80, 90 or even 120 points. When you're building your own Team Rating System you should consider whether or not you'll place some cap on the Actual Outcome measure.)
The equation I use in MARS to convert the actual (capped) game margin to my outcome measure is shown on the right. There are two parameters in this equation, x and m, which are set to 0.49 and 130 respectively in MARS. This "squashing" function, in conjunction with the margin cap at 78 points, converts actual game margins into Actual Outcomes with a range from a low of about 0.24 for a loss by 78 points or more to a high of about 0.68 for a win by 78 points or more. A draw yields a value of 0.5. One feature of this function is that it slightly penalises large losses more than it rewards large victories: the largest value of the function, recorded for maximal victories of 78 points or more, is only 0.18 higher than the value of recorded for a draw, while the smallest value, recorded for losses of 78 points or more, is 0.26 lower than the value recorded for a draw.
Any of a variety of other "squashing" functions might be used to map a chosen outcome variable onto the 0 to 1 interval or a portion of it, a couple of examples of which appear at right.
The top equation is the logistic and the bottom equation a modified version of an algebraic function. Each equation takes some actual outcome m, which may take on arbitrarily large positive or negative values, and maps it to the interval from 0 to 1.
Choosing a mapping function from the raw outcome measure to a version in the 0 to 1 range is one area where you can give full flight to your mathematically creative instincts, and one where I'd encourage you to try a number of functional forms until you find one appropriate for your needs.
Instead of choosing the game margin as your outcome variable, which you might think about as the difference between points scored and points conceded, you could choose another game statistic that lends itself to differencing such as the difference in the number of goals scored, the difference in the number of kicks recorded, or the difference in number of inside-50s achieved. Following this approach you could construct a set of Team Rating Systems, one for each of the metrics in which you're interested, the outputs of which you might then combine to derive an overall Team Rating.
Your choice of outcome metric is an important one, and one that you should resolve with a firm view of what you want your Rating System to achieve.
Share of Scoring
For today's blog I'm going to neatly sidestep the need for any transformation by using as my outcome metric the team's proportion of total points scored, a metric which is naturally bounded by 0 and 1. Despite this mathematical convenience I could, nonetheless, investigate transformations of a team's share of scoring but will, instead, in the grand tradition of lecturers and textbook authors everywhere, "leave this as an exercise for the reader".
One of the appealing aspects about this choice of metric in the context of VFL/AFL is that it is, unlike the victory margin outcome measure used in MARS, unaffected by the more-recent increases in scoring relative to the earlier portions of football history. With this metric, a team that scores 60% of the points in a game in which it takes part is accorded the same recognition by the resulting Rating System whether it achieved this result by winning 60 to 40 in the early 1900s or by winning 180 to 120 in the modern era.
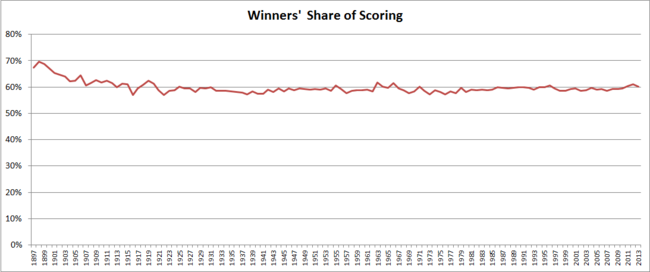
As I've commented on previously, the "winners' share of scoring" statistic has been remarkably stable from season to season across the vast majority of VFL/AFL history.
Since 1920, the season-average share of scoring by victorious teams has tracked in a narrow range from 57% to 61.7%, and from 1979 it's tracked in an even narrower range from 58.2% to 61%.
Step 2: Mapping Team Ratings to Expected Outcomes
Next we need to come up with a reasonable basis on which to estimate a team's expected outcome - for today's blog, its expected proportion of the total points scored - as a function of its own and its opponent's Rating.
Once again there are a huge number of functions we might choose for this purpose but here, faithful to the Elo tradition, we'll opt for something of the form shown at left.
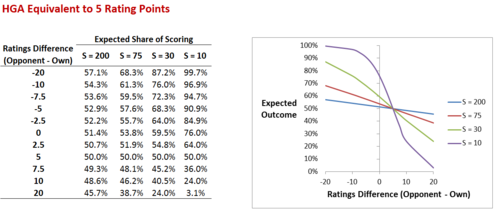
The parameter HGA in this equation represents the Home Ground Advantage, here measured in terms of the Ratings Points equivalent of the benefit to a team of playing at its home ground. The parameter S is a scaling parameter that controls the extent to which a team's Ratings deficit, net of any Home Ground Advantage, is translated into expected performance. Larger values of S mean that a team's Expected share of points scored responds more slowly to any given Ratings deficit or surplus net of Home Ground Advantage, while smaller values of S mean the opposite.
At left I've shown how the Expected share of scoring responds to differences in team Ratings as we vary S for a fixed value of HGA (here set to 5).
At small values of S, small changes in Ratings Difference correspond to large changes in Expected share of scoring. Conversely, at large values of S, equivalent differences in Ratings correspond to much smaller differences in Expected share of scoring. Since we've set the HGA to be worth the equivalent of 5 Ratings Points in the scenario tabled and charted here, all of the curves cross the 50% point for the Expected Outcome at the point where the Ratings Difference is exactly 5 Ratings Points. So, in words, a team Rated 5 points lower than its opponent would be expected to score 50% of the points in a contest (ie draw) if it were playing at home.
One of the areas that you might want to explore as you develop your own Rating System is the parameterisation of Home Ground Advantage. The formulation I've used here employs a single parameter, but you could instead have different, fixed values of HGA for each team, or even for each team at each venue. Alternatively you might, as MAFL does in the algorithms that underpin some of the Funds, treat Home Ground Advantage as a continuous value calculated based on the experience that the competing teams have had at the current venue in, say, the past 12 months. The essential role of the HGA parameter is to adjust the Actual Outcome to remove the beneficial effects of playing at home, leaving as a residual the true underlying ability of a team.
Step 3: Choosing the Optimal Parameters
For the Team Rating System as I've defined it so far, there are three parameters that we need to choose:
k, the parameter that converts differences between Actual and Expected Outcomes into changes in Ratings
HGA, the Home Ground Advantage, measured in terms of Rating Points equivalence
S, the divisor in the Expected Outcome equation that determines how nett Ratings differences are translated into expectations about the proportion of points scored
We need also determine the Rating that we'll apply to new teams. Essentially, this value functions as a scaling parameter, and I'll be setting it to 1,000 for today's blog, the same value that I use for MARS Ratings.
Now, if we plan to use our Team Rating System across seasons, there's one more parameter that we need to set, which is what I call the "Carryover" parameter. It determines how much of a team's Rating is carried from one season into the next. History tells us that teams' capabilities are autocorrelated, though not perfectly, across seasons, and the larger the value of the Carryover parameter, the larger we're assuming this correlation to be. The formula I've used here ensures that the average Team Rating is preserved at 1,000 from one season to the next - unless, of course, a team with a Rating of other than 1,000 leaves the competition, a quirk I had never realised about this approach until I started working on this blog. For reasonably large values of the Carryover parameter, the all-team Rating average does move back towards 1,000 relatively quickly after the exit of a team, but it never attains it. Possibly the only consequence of any note of this quirk in the context of the all-time MARS Ratings is that it might be seen as allowing teams to attain artificially high Ratings in the season directly following the exit of a relatively weak team since the pool of available Ratings Points will be higher per team than in the years preceding that team's exit.
The current MARS system uses a Carryover of 47%, which means that Team Ratings are dragged back towards 1,000 by an amount roughly equal to one half of the difference between their end-of-season Rating and the value 1,000.
Initial Team Ratings aside then, we need to choose values for 4 parameters: k, HGA, S and Carryover.
You could, entirely reasonably, simply select values you felt where appropriate for each of these parameters and then be on your way. A more empirical approach would be to choose optimal values for these parameters based on some fitness metric. Such a metric might be calculated directly from historical Ratings themselves - for example, how often the team with the higher Rating won - or they might depend on your building a secondary model with the Ratings as an input. For example, you might want to measure how good your Team Ratings are at allowing you to make well-calibrated probability estimates about the victory chances of teams.
I've chosen two metrics for the purposes of optimisation today: accuracy in selecting game outcomes (on the basis that we select as the winner in any game the team with the higher Rating at the time, regardless of home team status) and precision in estimating the proportion of points that a team will score (measured as the absolute difference between the estimated and actual scoring proportions, with the estimated proportion of scoring calculated using the Expected Outcome equation above).
For both of these metrics I've performed optimisations to select the best values of the four parameters under three scenarios, each of which reflects a different view on the relative importance of the Rating System performing well in recent seasons versus performing well in earlier seasons:
Scenario 1, in which outcomes for the period 1897 to 1939 are weighted at 10%, for the period 1940 to 1969 are weighted at 20%, for the period 1970 to 1999 are weighted 25%, and for the period 2000 to 2013 are weighted 45% (ie the predictions for more recent eras matter more than those for long-forgotten eras, but we still care a little about the efficacy of our Ratings System at the turn of the previous century).
Scenario 2, in which the weights are, instead 0%, 0%, 50% and 50% respectively (ie all that matters are the predictions for the periods 1970 to 1999 and 2000 to 2013, each of which matters equally).
Scenario 3, in which the weights are, instead 0%, 0%, 0% and 100% respectively (ie all that matters are the predictions for the period 2000 to 2013).
I used Excel's Solver capabilities to estimate the "optimal" parameter values in all of these scenarios, the results of which are recorded in the following table. (I put "optimal" is quotes because I doubt that the values Excel gave me are the best of all possible values. I'm fairly confident they're near-optimal however.)
So, for example, a Ratings System that is acceptably accurate across the entire span of VFL/AFL history (ie with era weights of 10/20/25/45) would use a k of 5.25, an HGA of a little over 2, a value of S equal to 38.71, and a season-to-season Carryover of 56.3%. These values produce a Team Ratings System that would have correctly predicted game outcomes 68.3% of the time on a weighted basis.
Focussing instead on more-recent eras but still employing Accuracy as our metric would lead to much larger values of k, HGA and S. We could, for example, have correctly predicted the result of almost 68% of games across the entire period from 2000 to 2013 by adopting values of k equal to about 35.6, HGA equal to about 9, S equal to a little less than 250, and a Carryover value of about 57.5%.
If, instead, we chose as our Team Rating System performance metric the absolute difference between the actual and expected proportion of points scores, then the optimal values of the four parameters would be quite different, though less so if our focus was solely on the most-recent era from 2000 to 2013 where the found optimal values were about 38.5 for k, 8.5 for HGA, 242.3 for S, and 53% for the Carryover.
Summary
In constructing your own Elo-style Team Rating System you need to:
choose an outcome metric, which here I've recommended be a metric bounded by 0 and 1, monotonically increasing with improved performance
choose a formula to map Team Ratings to expected outcomes, accounting for other factors such as Home Ground Advantage
determine the perfomance metric you'll use to assess the efficacy of any set of parameters
find optimal parameter values on the basis of that metric using either the entirety of VFL/AFL history as I've done here or, instead, by estimating the optimums using a subset of games and then assessing performance on a holdout set
That's all there is to it.
One aspect of creating Elo-style Rating Systems for VFL/AFL that I've found intriguing has been the tendency for different optimised Systems to produce highly correlated Team Ratings. For example, all of the Systems I built for this blog are correlated at least +0.95 with the standard all-time MARS Ratings. This is possibly due to the similarity in the performance metrics I've used to create all of these Systems; it would be interesting to see if a more exotic metrics - say, for example, efficacy in wagering - produced less-correlated Ratings.