Estimating Fair Head-to-Head Prices : Part II
/In the previous blog on this topic I described a way to estimate the vig embedded in the head-to-head prices of both teams in a contest by assuming that:
- Handicap-adjusted Margins (HAMs), created using the handicaps posted by the TAB Sportsbet bookmaker and calculated from the viewpoint of the Favourite, can be approximated by a Normal distribution
- These HAMs have zero mean
- These HAMs are of constant variance across games (ie are homoscedastic)
An initial analysis led me to believe that those last two assumptions were reasonable, but further work has hinted that the mean and variance might vary over the range of handicaps.
But, I'm getting ahead of myself. First let me explain the data I'll be using in this blog.
Filtering the Data
The methodology described in that earlier blog should logically only be applied to contemporaneous information from the line and head-to-head markets. Most of the wagering data I have meets that requirement, but for those games where the line market was posted after the day on which I lock in MAFL wagers it's possible that the head-to-head prices will have drifted before the line market is posted. In these cases my data will consist of the head-to-head prices at the time I locked in the MAFL wagers (usually noon on the Wednesday before the game takes place) and the line details at whatever time they were first posted.
Post hoc it's impossible for me to identify these games unless the drift in the head-to-head prices has been especially dramatic. Games where the drift has been sufficient to be apparent in hindsight are the first set of games that I've tried to exclude from the analysis. My rule for detecting these games was that the handicap posted was 12.5 points or less and was more than 5 points different from what I would have expected given the head-to-head prices. To come up with an expected handicap I used the formula -22.3*ln(Underdog Price/Favourite Price), which I developed in an earlier blog.
I also excluded any game where the start offered implied a switch in favouritism compared to the head-to-head prices (ie the favourite in terms of the head-to-head prices wound up receiving start in the line market).
Finally, we also need to ensure that we only include games where the handicap posted was intended to produce a HAM of zero, which is not the case where the handicap is posted with different prices for each team in the line market. You'll recall that this was a common occurrence in the past for games that should have had handicaps under 6.5 points. I have, therefore, excluded all games with a handicap of 6.5 points or less, except if those games were from season 2012 when the practice has been to offer "proper" handicaps - that is, a handicap of less than 6.5 points - and to offer the same line price for both teams.
In summary then, I've excluded games where:
- the handicap is so incongruous with the head-to-head prices that it suggests the respective teams' chances had altered between the time the head-to-head market was locked in by MAFL and the time the Line market was posted
- the handicap suggests that favouritism had switched between the time the head-to-head market was locked in by MAFL and the time the Line market was posted
- prices on the Line market were not equal for both teams, meaning that the handicap had been artificially set at 6.5 points and team prices manipulated to achieve equality
Combined, these exclusions reduce an original set of 1,216 games to 985 that we analyse.
A Closer Look at Favourite HAMs (or Porky Pig, for those old enough to get this reference)
The mean HAM from the Favourite's perspective for those 985 games is -0.31 points per game which, statistically speaking, is not significantly different from zero, and the standard deviation about that mean is 37.2 points per game. Based on those figures, the assumption that I made in the previous blog that HAMs were N(0,37.2) seems reasonable.
But a closer look at the Favourite HAM data reveals that Favorites giving between about 4 and 8 goals start have been returning positive HAMs, and Favourites giving starts in other ranges have been returning negative HAMs. To put some numbers on this:
- Favourite HAMs in games where Favourite gives less than 4 goals start
- Mean HAM = -2.53 points
- SD HAM = 36.7 points
- Favourite HAMs in games where Favourite gives more than 4 but less than 8 goals start
- Mean HAM = +4.88 points
- SD HAM = 37.3 points
- Favourite HAMs in games where Favourite gives more than 8 goals start
- Mean HAM = -7.06 points
- SD HAM = 39.4 points
One way to apply the approach I developed in the previous blog would be then to assume that Favourite HAMs come from one of three Normal distributions with the means and standard deviations shown here, the correct one to use for estimating the victory probability of the Favourite in any particular game depending on the handicap set for that game.
If, for example, the Favourite was giving 12.5 points start then the correct Normal distribution to use would be N(2.53, 36.7). If, instead, the Favourite was giving 30.5 points start then we'd use the N(-4.88, 37.3) distribution, and if the Favourite was giving 52.5 points start we'd use the N(7.06, 39.4). (The change in sign for the mean is to negate the advantage or disadvantage for the Favourite as measured in the historical HAM measurements.)
The following chart shows, for the full range of handicaps, the estimated victory probability for the Favourite if we adopt this tri-distributuion approach (the dotted line). The chart also shows the victory probability estimates that we'd obtain if we assumed instead a single N(0.37.2) distribution across the range of handicaps (the green line).
The chart also shows two other things: the actual winning percentage of Favourites at each handicap (the purple dots), and the probability estimates obtained by following a more direct approach (the red line). I'll come back to the red line in a moment.
In the meantime though note the sharp inflection point in the purple dots at around the 20-30 point range where the empirical victory probability for Favourites leaps from about 60% to 80%. The green line, representing the N(0,37.2) assumption fails to rise quickly enough to map to this empirical reality while the dotted line, representing our three-part mixed Normal model, does a much better job, though still seems to somewhat underestimate the Favourite's chances in the 30-50 point range.
An Empirical Model
To come up with the even-better fitting red line in the chart above I gave up the attraction of assuming that HAMs were Normal and, instead, decided to fit a smooth function to the empirical Favourite victory percentages. For this task I used Eureqa, splitting the data into 50% training and 50% validation sets, specified a logistic functional form and a squared error metric, excluded the 12 games from 2012 with a handicap under 7 points as they seemed to be having a distorting influence, and then watched as Eureqa came up with this:
Probability of Favourite Victory = logistic(logistic(24.33 - Handicap) - 0.02928 x Handicap)
This nifty functional form, with the nested logistics, yields the red line in the chart above.
Using this line we can calculate an estimate of the fair head-to-head price for the Favourite in any given game and, if we assume a flat 1% probability of a draw in every contest, a fair head-to-head price for the Underdog too. Given these two values we can then estimate the vig on the Favourite and the Dog in the head-to-head market for each contest.
If we average these calculations for every game with the same handicap, we obtain the following chart:
What we see for the Underdog is, on average, huge levels of vig in games where the handicap is more than about 4 goals, and smaller, even negative average vigs for games with smaller starts. In contrast, Favourites show relatively low but mostly positive levels of average vig for handicaps of about 5 goals and above, and then a sharp increase in vig at lower handicaps, tapering off as handicaps tend to zero.
There's some commonsense in the lower levels of vig on Favourites at high handicaps when you recall that the bookmaker, to make a guaranteed profit, requires that the proportion of wagers on the favourite be inversely proportional to the Favourite's head-to-head price. So, when the Favourite's price is very low, the bookmaker needs to find a way to make the proportion of wagers on the Favourite relatively high.
Negative Vig Wagering
Had we known in 2006 what we now know through the miracle of hindsight and significant computing power, we could have used this model to identify those teams whose head-to-head price seemed to be carryiing negative vig - in other words, was generously high given the team's estimated probability using this model.
Our results would have been as follows:
Across the 7-and-a-halfish seasons we'd have made 146 wagers on Favourites and only on (some of) those Favourites giving between 24.5 and 44.5 points start on Line betting. These wagers would have produced a 1.6% ROI.
We'd also have made over twice as many wagers on Underdogs, and only on Dogs receiving between 7.5 and 23.5 points start. From the 314 wagers of this type we'd have cranked out an 11.1% ROI. At about 1 wager in every 3 games it would have been a slow accumulation, but it would have been sweet nonetheless.
As you see from the chart at right, which shows the estimated vig and the actual head-to-head price of the Favourite in every game in our sample, most of the wagers on Favourites would have been placed at prices of between about $1.10 and $1.25. That's quite a narrow range.
It's interesting to note how the vig spikes for Favourites in the $1.30 to $1.60 range, which certainly accords with my recollection of many lost wagers in recent seasons on teams in this price range.
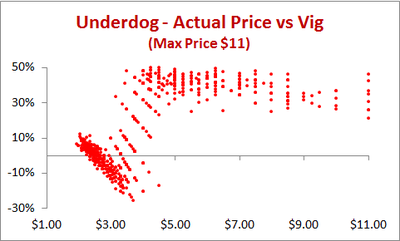
The same chart, but this time for the Underdogs reveals that the negative vig opportunties for these teams comes at prices in about the $2.50 to $4.50 range.
Vigs as low as -25% can sometimes be spotted in this price range.
Once a Dog is priced above about $5 though, the vig becomes prohibitive. Making money in the long-term wagering on Underdogs priced at these levels would require incredible skill, indescribable luck, or a potent mix of both.
(Those of you with long-standing MAFL-scars will no doubt be recalling the often painful days of the Heritage Fund, which fancied its chances making money on Dogs in this price range. The occasional large payouts for this Fund were usually book-ended by a slew of unsuccesful wagers that not even fervid supporters would make.)
Empirical (and Historical) Fair Prices
To finish, here's a lookup table showing the fair price for the Favourite and the Underdog given the handicap being offered in the Line market by the TAB Sportsbet bookmaker. I'd caution strongly against using this as a basis for actual wagering because it's success has been demonstrated only on within-sample games. Even then, it would not have produced a profit in every season, losing money in aggregate in 2008 and in the current season to date. Better, I'd suggest, to keep an eye on its performance over the remainder of this season.
* assuming a 1% probability of a draw for all games