Probability Scoring Methods
/In Sunday's blog I introduced the three probability scoring methods that I'll be using to evaluate the HELP model's predictive performance this season.
To recap, they were:
The logarithmic score, which assigns a forecaster a score of 2+log(p) where p is the probability that he or she assigned to the winning team.
The quadratic score, which assigns a forecaster a score of 1-(1-p)^2 where p is again the probability that he or she assigned to the winning team.
The spherical score, which assigns a forecaster a score of p/sqrt(p^2 + (1-p)^2), where p is yet again the probability that he or she assigned to the winning team.
These measures have been devised over four or five decades to answer the seemingly simple question of which set of probability forecasts for a given set of events is best in light of later knowledge of whether the events to which the forecasts pertained occurred or did not occur.
The logarithmic score is very commonly used in the literature and has empirical support for its superiority in some circumstances. I even read of one teacher who insisted that his students assign probabilities to each of the four suggested answers in a multiple choice test and then used the logarithmic score to grade the papers.
This scoring method is problematic - as that teacher might well have discovered - whenever a forecaster assigns a probability of zero to some event that occurs (or of one to an event that doesn’t occur) because, in that case, the resulting score will be negative infinity at which point things just get silly. Infinity is a bit like the Hotel California: once you've checked in you can never leave. Some users of the logarithmic scoring method fudge this situation by assigning probabilities of 0.01 where a forecaster has chosen a probability of 0, and 0.99 where a forecaster has chosen a probability of 1, but that's the sort of ad hocery that gives the practice a bad name.
Fortunately, in our case this quirk of the logarithmic score will not be a problem since HELP will never forecast a probability of 0 or 1.
Another feature of the logarithmic measure is its tendency to punish forecasters particularly severely if they forecast below about 20% for an event that actually occurs. Consider, for example, that a forecaster assigning a probability of 50% to an event that occurs scores 1 (the logs, by the way, are traditionally done base 2), another forecaster who assigns 35% to that same event scores 0.49, but one who assigns 20% to it scores -0.32.
The quadratic score - also known as the Brier score - has the good manners to always provide a score between 0 and 1, though it is asymmetric in that a forecaster receives a score halfway between the best and the worst possible scores when he or she assigns a probability of 30% to an event that occurs.
The spherical score, probably the least used of the three measures, also produces scores bounded by 0 and 1 and it too is asymmetric, though it gives half marks for a probability of around 37%, which is slightly closer to 50% than is the case for the quadratic score.
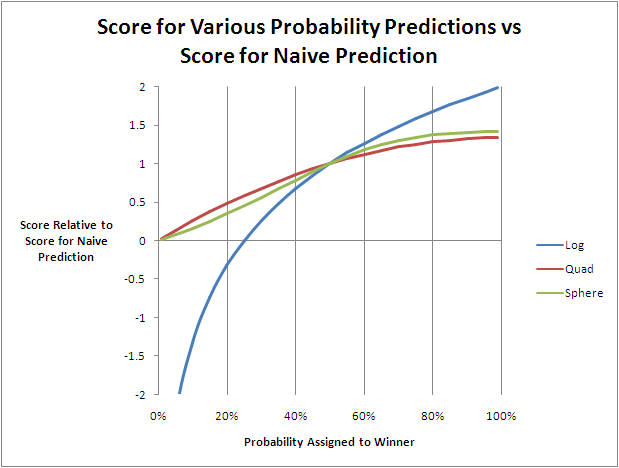
A useful way to compare the three scoring methods is to consider the scores they give to tipsters providing various probabilities for an event that occurs relative to what that same method gives for a naive forecaster who always predicts 50%.
Since the values shown in the chart are all relative to the score given for a 50% probability prediction, all three lines attain a value of 1 when the probability is 50%.
What's clear from this chart is how much more discriminating is the logarithmic method. It punishes and rewards forecasts below and above 50% much more than do either of the other methods. The spherical method is the next most discriminating, and the quadratic method is the least discriminating, or kindest if you prefer, of all.
One final feature to note about all three scoring methods is that they reward "truthfulness" - that is, if you think the probability of an event is X% then you'll maximise your score in the long run by predicting a value of X%.
(Since we're on the topic of probability scoring, I note in passing that I did the HELP model an injustice last weekend in that I made its predictions using some dummy data for Round 1 that I had mocked up while preparing for the season rather than using the actual data for Round 1.
I did the same thing to HAMP and LAMP.
Here then are the corrected results for HELP, HAMP and LAMP.
You'll notice that HELP now did in fact outpredict a naive forecaster. Mea culpa.
This correction has done wonders for HAMP's and LAMP's mean APE and has also boosted HAMP's median APE.
I chalk these errors up to first round nerves ...)